와챠의 우당탕탕 코딩 일기장
[알고리즘] 스파르타 코딩 : 알고리즘 - 4주차 본문
힙

트리 : 뿌리와 가지로 구성되어 거꾸로 세워놓은 나무처럼 보이는 계층형 비선형 자료구조
ㄴ선형구조 : 자료를 구정하있는 데이터들이 순차적으로 나열된 형태(큐, 스택)
ㄴ자료의 저장/꺼내기에 초점
ㄴ비선형 구조 : 데이터가 계층적 혹은 망으로 구성됨
ㄴ표면에 초점
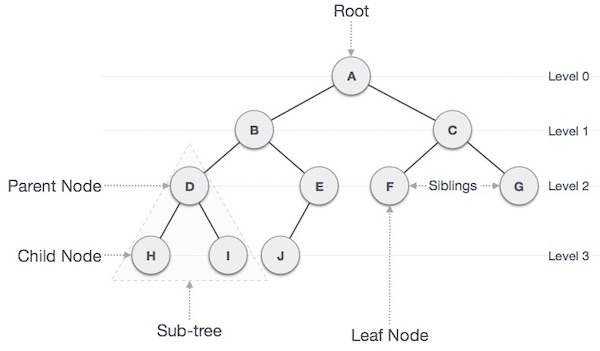
트리 용어 정리
Node: 트리에서 데이터를 저장하는 기본 요소
Root Node: 트리 맨 위에 있는 노드
Level: 최상위 노드를 Level 0으로 하였을 때, 하위 Branch로 연결된 노드의 깊이를 나타냄
Parent Node: 어떤 노드의 상위 레벨에 연결된 노드
Child Node: 어떤 노드의 하위 레벨에 연결된 노드
Leaf Node(Terminal Node): Child Node가 하나도 없는 노드
Sibling: 동일한 Parent Node를 가진 노드
Depth: 트리에서 Node가 가질 수 있는 최대 Level
트리의 종류
- 이진 트리 : 각 노드가 최대 2개의 자식을 가짐
- 완전 이진 트리 : 노드 삽입 시 맨 왼쪽 노드부터 차례로 삽입
o Level 0
o o Level 1
o o Level 2 # -> 이진 트리 O 완전 이진 트리 X
o Level 0
o o Level 1
o o o Level 2 # -> 이진 트리 O 완전 이진 트리 O
트리에서 부모와 왼쪽, 오른쪽 자식 구하기
부모의 인덱스 : 현재 인덱스 // 2
왼쪽 자식의 인덱스 : 현재 인덱스 * 2
오른쪽 자식의 인덱스 : 현재 인덱스 * 2 + 1
완전 이진 트리 구현
# 최댓값 힙
# 최댓값의 추가/삭제 및 정렬이 빠르게 이루어짐
class MaxHeap:
def __init__(self):
self.items = [None]
# 완전 이진트리의 최대 높이인 O(logN)
def insert(self, value):
# 배열 끝에 삽입
self.items.append(value)
# 삽입한 위치 인덱스 구하기
cur_index = len(self.items) - 1
# 루트 노드까지 반복
while cur_index > 1:
# 부모 인덱스 구하기
parent_index = cur_index // 2
# 부모 노드 < 자식 노드면 교환
if self.items[parent_index] < self.items[cur_index]:
self.items[parent_index], self.items[cur_index] = self.items[cur_index], self.items[parent_index]
cur_index = parent_index
# 부모 노드가 더 크면 반복 끝
else:
break
# 완전 이진트리의 최대 높이인 O(logN)
def delete(self):
# 루트 노드와 마지막 노드 교환
self.items[1], self.items[-1] = self.items[-1], self.items[1]
# 최댓값 데이터 저장
# 데이터 삭제
delete_date = self.items.pop()
cur_index = 1
# 제일 마지막 노드까지 힙 규칙 따르기
while cur_index <= len(self.items) - 1:
left_index = cur_index * 2
right_index = cur_index * 2 + 1
# 현재 노드 값, 왼쪽 자식 값, 오른쪽 자식 값 중 가장 큰 값의 인덱스
max_index = cur_index
# 왼쪽 자식이 존재하고 부모보다 크다면
if left_index <= len(self.items) - 1 and self.items[left_index] > self.items[max_index]:
max_index = left_index
# 오른쪽 자식이 존재하고 부모보다 크다면
if right_index <= len(self.items) - 1 and self.items[right_index] > self.items[max_index]:
max_index = right_index
# 현재 인덱스가 자식보다 크면 반복 종료
if max_index == cur_index:
break
# 현재 값과 가장 큰 값 변경
self.items[cur_index], self.items[max_index] = self.items[max_index], self.items[cur_index]
return delete_date # 8 을 반환해야 합니다.
max_heap = MaxHeap()
max_heap.insert(8)
max_heap.insert(6)
max_heap.insert(7)
max_heap.insert(2)
max_heap.insert(5)
max_heap.insert(4)
print(max_heap.items) # [None, 8, 6, 7, 2, 5, 4]
print(max_heap.delete()) # 8 을 반환해야 합니다!
print(max_heap.items) # [None, 7, 6, 4, 2, 5]
level k에 최대로 들어갈 수 있는 노드 개수 : 2의 k승
1 Level 0 -> 1개
2 3 Level 1 -> 2개
4 5 6 7 Level 2 -> 4개
8 9....... 14 15 Level 3 -> 8개
Level k -> 2^k 개
높이가 h이고 모든 노드가 꽌 차있는 완전 이진트리에서 모든 노드의 개수 : 2의 (h+1)승 - 1
1 + 2^1 + 2^2 + 2^3 + 2^4 ..... 2^h
최대 노드 갯수 N, 높이 h라면,
2의(h+1)승 - 1 = N
=>h = log2의(N+1) - 1
상수 제외 => 이진 트리의 최대 높이 = O(logN)
DFS(Depth First Search, 깊이 우선 검색), BFS(Breadth First Search, 넓이 우선 검색)

DFS : 자료의 검색, 트리나 그래프를 탐색하는 방법.
한 노드를 시작으로 인접한 다른 노드를 재귀적으로 끝까지 탐색하면, 다시 위로 올라와서 다음을 탐색.
ㄴ공간 적게 씀(그래프의 최대 깊이만큼 공간 필요)
BFS : 한 노드를 시작으로 인접한 모든 정점들을 우선 방문하는 방법.
ㄴ최단 경로 쉽게 찾을 수 있음
ㄴ공간 많이 차지함
ㄴ시간 더 오래 걸림
DFS 구현 : 재귀 함수
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
# 딕셔너리로 인접 노드 표현
graph = {
1: [2, 5, 9],
2: [1, 3],
3: [2, 4],
4: [3],
5: [1, 6, 8],
6: [5, 7],
7: [6],
8: [5],
9: [1, 10],
10: [9]
}
visited = []
# 재귀 함수로 구현
def dfs_recursion(adjacent_graph, cur_node, visited_array):
# 방문 기록하기
visited_array.append(cur_node)
# 인접 노드 방문하기
for adjacent_node in adjacent_graph:
# 방문한 적 없는 노드면 방문하기(탈출 조건 역할)
if adjacent_node not in visited_array:
dfs_recursion(adjacent_graph, adjacent_node, visited_array)
return
dfs_recursion(graph, 1, visited) # 1 이 시작노드입니다!
print(visited) # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 이 출력되어야 합니다!
DFS 구현 : 스택 - 가장 마지막에 넣은 노드 탐색
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
1: [2, 5, 9],
2: [1, 3],
3: [2, 4],
4: [3],
5: [1, 6, 8],
6: [5, 7],
7: [6],
8: [5],
9: [1, 10],
10: [9]
}
# 스택으로 구현
def dfs_stack(adjacent_graph, start_node):
stack = [start_node]
visited = []
# 스택이 비지 않을 때까지 반복
while stack:
# 현재 노드 꺼내기
current_node = stack.pop()
# 방문 기록 남기기
visited.append(current_node)
# 현재 노드에 인접한 노드들 접근
for adjacent_node in adjacent_graph[current_node]:
# 가보지 않은 곳이면 방문하기
if adjacent_node not in visited:
stack.append(adjacent_node)
return visited
print(dfs_stack(graph, 1)) # 1 이 시작노드입니다!
# [1, 9, 10, 5, 8, 6, 7, 2, 3, 4] 이 출력되어야 합니다!
BFS 구현 : 큐 - 가장 처음 넣은 노드 먼저 탐색
# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
1: [2, 3, 4],
2: [1, 5],
3: [1, 6, 7],
4: [1, 8],
5: [2, 9],
6: [3, 10],
7: [3],
8: [4],
9: [5],
10: [6]
}
def bfs_queue(adj_graph, start_node):
queue = [start_node]
visited = []
# 큐이 비지 않을 때까지 반복
while queue:
# 맨 앞 노드 꺼내기
current_node = queue.pop(0)
# 방문 기록 남기기
visited.append(current_node)
# 현재 노드에 인접한 노드들 접근
for adjacent_node in adj_graph[current_node]:
# 가보지 않은 곳이면 방문하기
if adjacent_node not in visited:
queue.append(adjacent_node)
return visited
print(bfs_queue(graph, 1)) # 1 이 시작노드입니다!
# [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 이 출력되어야 합니다!DP(Dynamic Programming, 동적 계획법) : 부문 문제의 해를 통해 전체 문제를 해결하는 방법
ㄴ결과를 기록 : 메모이제이션(Memoization), 문제를 쪼갤 수 있는 구조 : 겹치는 문제(Overlapping Subproblem)
피보나치 수열 : 1,1,2,3,5... => Fibo(n) = Fibo(n - 1) + Fibo(n-2)
피보나치 수열 DP로 구현
input = 50
# memo 라는 변수에 Fibo(1)과 Fibo(2) 값을 저장해놨습니다!
memo = {
1: 1,
2: 1
}
def fibo_dynamic_programming(n, fibo_memo):
if n in fibo_memo:
return fibo_memo[n]
nth_fibo = fibo_dynamic_programming(n-1, fibo_memo) + fibo_dynamic_programming(n-2, fibo_memo)
fibo_memo[n] = nth_fibo
return nth_fibo
print(fibo_dynamic_programming(input, memo))'이런 저런 공부' 카테고리의 다른 글
| [알고리즘] 스파르타 코딩 : 알고리즘 - 5주차(완강) (0) | 2021.07.25 |
|---|---|
| [알고리즘] 스파르타 코딩 : 알고리즘 - 4주차(숙제) (0) | 2021.07.16 |
| [알고리즘] 스파르타 코딩 : 알고리즘 - 3주차(숙제) (0) | 2021.07.10 |
| [알고리즘] 스파르타 코딩 : 알고리즘 - 3주차 (0) | 2021.07.09 |
| [알고리즘] 스파르타 코딩 : 알고리즘 - 2주차 (0) | 2021.07.08 |



